1 Why develop a new theory?
This web site introduces a new approach to analyzing hierarchical organization in nature: ‘The Operator Theory’. The theory is based on physical entities called ‘operators’. The abbreviation O-theory is used to distinguish it from mathematical operator theory. Before diving in, I will explain why this theory was developed.
Scientists use ‘levels of organization’ when analyzing complexity in ecology and nature. Typically, such levels are chosen in relation to specific research goals. This is practical, for example, if you want to analyze a food chain, or how toxic chemicals affect cells, organs, organisms, and populations. However, when ranking levels, one can also ask: What is a ‘level’? When does a level begin or end? What separates entities on one level from those on the next? And maybe you want to ask a deep scientific question like Is it possible for a hierarchy to have fixed levels, and could these be extrapolated? In the winter of 1993-1994, I searched textbooks for answers to such questions and discovered something interesting. Classical textbooks typically rank ecological hierarchies using a mixture of rules for successive levels. A common example is
Classical approach: cell → organ → organism → population
This is a common way of organizing complexity in ecosystems. But this ranking led me to ask a simple question: Is the ranking ‘consistent’? I chose two criteria for consistency: 1. A ranking includes objects of the same general type (e.g. ‘physical units’) at all levels. 2. A ranking uses the same rule to get from one level to the next. It came as a surprise that the above ranking fails both criteria (more about why in the next two paragraphs). These questions and goals helped me identify a series of innovations that catalyzed the development of O-theory. In particular, I hoped to find a way to create a hierarchy with fixed levels that could be extrapolated.
2 Are the objects of the same general type?
To allow extrapolation, a hierarchy should be “consistent”. As explained above, this means that all entities are of the same major type, and that all steps in the hierarchy are of the same major type. In this section, I will examine the consistency of the use of object types in the classical hierarchy. The types of ranking relationships are discussed below.
What are the types of entities in the classical hierarchy presented above?
Classical approach: cell => organ => organism => population
Cell: On the one hand, a cell is a physical unit. On the other hand, the term ‘cell’ refers to many physical objects at once: a single cell (such as a bacterium), a mitochondrion in a eukaryotic cell, a eukaryotic cell, or a eukaryotic cell in a multicellular organism.
Organ: An organ is a multicellular unit that typically is a part of a multicellular organism. Organs do not form from aggregating cells, but form within a multicellular organism during its development.
Organism: The term organism refers to a broad conceptual class, that contains e.g. bacteria, protozoa, plants/fungi and animals. Some also consider lychen, or the slug of a slime mould, to be an organism. There is currently no universally accepted definition of the term organism, which makes it problematic to use the term in a consistent hierarchical ranking.
Population: A population refers to a particular group of organisms. In principle, the members of a population live in the same area (although some may leave and others may enter). Organisms in a population belong to the same species. The concept of ‘species’ has proved difficult to define strictly. In general, people use common descent (question: how far back should common descent go?), combine this with the ability to mate successfully with at least one nearby member of the group (question: must we exclude organisms in a population that do not mate successfully?). Mating outside the group must be rare (question: how rare is ‘rare’?). Because of such considerations, the species concept is an idealization that is not completely watertight at its edges. Most importantly, however, the population is a concept that refers to a grouping, not to a physical thing. For example, a population as such cannot drink or eat.
Wrapping up:
The entities in the above hierarchy belong to different logical types, e.g.:
- A cell = a physical object or part of an object
- An organ = an integral structural and physiological part of a multicellular organism
- An organism = a broad conceptual class that includes biological entities of varying complexity
- A population = a conceptual grouping of organisms of the same species.
3 Are the ranking relationships op the same general type?
Above I explained that in a consistent hierarchy all steps to a next level should be of a similar main type. For example: entities of level N form the entity of level N+1. Does this criterion hold for the standard classical ranking?
Although the classical ranking does not make this explicit, the first three steps focus on how a multicellular organism, as a single multicellular organism can be decomposed into parts. It would be more correct, therefore, to start the ranking at the organism level and work ‘inwards’: organism => organ => cell. The step towards a population, then, is different. This is because the interactions between the organisms in the population don’t cause a single, bounded, physical entity. A population is a conceptual grouping of autonomous individuals. The ranking therefore starts with physical organisms of one species and continues with their grouping (theoretically) into a ‘population’. The ranking points from organism to a conceptual group. The result is: organism => population. The grouping relationship differs from the ‘is a part of’ relationship!
Wrapping up:
The analysis of our example ranking shows that the classical rules for connecting entities at successive levels are not the same between levels (e.g. ‘is part of’ versus ‘is a conceptual grouping of’). Furthermore, the relationships can’t always be precisely defined, because the entities at the different levels can’t always be precisely defined, and vice versa.
The above theoretical obstacles raise the question of whether the classical ranking can serve as a basis for a consistent theory of hierarchical organization in nature. In a pessimistic scenario, we are stumbling around in a conceptual fog that prevents us from recognizing and resolving fundamental questions about the definitions of widely used terms in biology and ecology.
4 Three rankings
The classic picture of an ecological hierarchy is that of a linear ranking. The above has shown that existing linear rankings tend to mix different kinds of entities while applying different kinds of ranking rules. As an innovation, I propose to place organisms in the center and analyze hierarchy along three dimensions: inwards, outwards and upwards.
1: The ‘inward’ dimension.

Hierarchy within an organism
For example, if we look at a horse, the organization inside it, its ‘internal organization’, can be analyzed in different ways. Interestingly, the nature of the relationships you observe between the same parts of the horse depends on your perspective.
Here I propose to group all the possible perspectives into four main groups: Displacement, Information, Construction, and Energy (acronym: DICE).
- From a displacement perspective, the focus is on the displacement of the horse itself and the displacement processes that occur inside the horse, e.g. the transport of food through the digestive system, the transport of blood through the body, the air flows in the lungs, etc.
- From an informational point of view, the focus would be more on the horse’s perception, the signals transmitted by its nervous system, the responses of its muscles.Another information perspective would be to focus on chemical signals based on hormones.
- From a constructional perspective, the horse has muscles, skin, bones, intestines, tissues, cells, etc.
- From an energetic point of view, we can classify the ingestion of food, its grinding in the mouth, its digestion in the stomach and intestines, the absorption of energy-rich molecules in the intestines, the transport of these molecules through the blood, and so on.
Each ranking gives rise to its own web of relationships. If a hierarchical arrangement is discovered using one DICE perspective, this will almost certainly change if you adopt a different DICE perspective. The implication is that hierarchy within any organism is a relative thing, depending on one’s perspective.
2: The ‘outward’ dimension.
Hierarchy as a result of organizing organisms according to increasingly inclusive interactions.
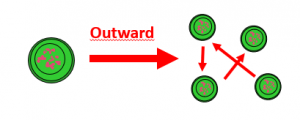
Let’s say you’re studying a group of organisms of some kind, such as horses. You might be interested in how a stallion guards different mares. And when a foal is born, how the mother and an aunt guard the foal during its first steps. Or how the foal drinks with her mother. Again, such interactions can be analyzed according to the four DICE perspectives. The displacement perspective focuses on how the mother and aunt actively shield and push away the stallion of the group. The information perspective focuses on how the horses interact through noise, smell, posture, etc. Drinking milk combines the energy and construction dimension.
A system resulting from interactions between organisms is called an ‘interaction system’ in OT. The reason for this naming is that the system consists of interacting organisms without being an organism itself. Basically, the OT distinguishes between two kinds of interaction systems: composite objects and groups.
3: The ‘upward’ dimension.
Hierarchy that results when organisms repeatedly give rise to more complex organisms of the next type
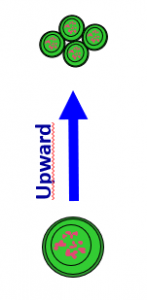
When organisms interact, they produce all sorts of systems. A very special subset of all such systems are the systems that are themselves an organism. By successive integrations, nature can produce increasingly complex organisms. When it comes to analyzing hierarchy, the sequence of organisms with increasingly complex blueprints has a distinct theoretical relevance: it has logical consistency. What I mean is that each subsequent organism type needs the properties of the preceding organism type as a basis. Such step by step hierarchical dependency is the backbone of the biological and physical part of the operator theory, and is explained in the next section.
5 Dual closure and unity
The O-theory is based on a special type of organization called a ‘loop’. A loop is formed when the last element in a series interacts with the first, ‘closing’ the loop. A loop has binary logic: it is either closed or open. When a loop closes, the system reaches a new configuration that provides a criterion for the ‘unity’ of the interacting elements.
A nice example of a loop is a group of people sitting on each other’s laps, so that the ‘last’ person is sitting on the lap of the ‘first’ person (this example is from Hofstadter’s book: “I am a strange loop”). The loop form implies a closed series of people sitting on each other’s laps, while at the same time a closed series of ‘lapping’ people implies a loop form: the mechanism implies the form, and the form implies the mechanism. Instead of the term ‘loop’, I follow many seminal international publications by using the term ‘closure’. A system has closure if one can identify a loop of interactions that cause a closed process and/or form.
There is something special about closure: a system either has it or it does not. A loop cannot be half closed. To be closed, a loop must have no missing links in its processes or in the elements that make it up. If there is a single missing link, the loop is not closed. Because of this, closure is an either/or property. It is a binary property. A binary property is of great theoretical value. It can be used as a strong criterion for identifying a (new) type of organization. This is why closure is used to identify every ‘basic unit’ in operator theory.
In fact, operator theory does not use just a single closure for each next layer, but two closures and their interaction. The combination of these criteria is called a ‘dual closure’, because the two closures form the minimal basis:
- Process closure (functional)(e.g. the set of autocatalytic molecules in a bacterium)
- Spatial closure (structural)(e.g. the membrane surrounding the bacterium.
A bacterial cell provides an example of the obligatory interaction between process and spatial closure. Here, the membrane holds together the set of autocatalytic molecules, and the set of autocatalytic molecules produces material for the membrane.
Succession and uniformity.
In addition to the above criteria, the O-theory uses several criteria to describe the subsequent transitions in the operator hierarchy in more detail. One of these criteria is that a dual closure must result from interactions between operators of the highest possible preceding level. Firstly, the ‘preceding level’ ensures uniformity in the nature of the operators involved in producing the next dual closure. Secondly, this use of the ‘highest preceding level’ ensures that each step in the ranking represents the shortest possible step to any next dual closure. In general, the highest preceding level will be level N-1 (e.g. the autocatalytic set and the membrane of a bacterium consist of molecules). Only in the atom does it refer to hadrons (level N-1) and electrons (level N-2).
The above criteria allow the construction/identification of a long series of successively formed operators. The name of this series is: the operator hierarchy. Interestingly, the operator hierarchy is not a simple ranking, because it has an internal structure. Although this is a very interesting topic, it requires a substantial explanation. This is beyond the scope of this website. For simplicity reasons, I will present the diagram while indicating ‘similarly based’ operator, grouped in so called ‘clusters’. The first cluster is that of the hadrons (such as protons and neutrons). The second cluster contains the atoms and molecules. The third cluster contains the following operator types based on cells: The cell (e.g. bacteria and archaea), multicellular organisms (e.g. bluegreen algae and streptomyces), eukaryotic cells, called ‘hostcells’ in O-theory (e.g. protozoa) and eukaryotic multicellulars (e.g. plants, algae, fungi). The fourth cluster so far only contains the organisms with a neural network, called ‘memons’ in O-theory (such as a fish, an earthworm and a human being). Those who wish to learn more should read recent publications on the O-theory (see the tabs: books or articles).
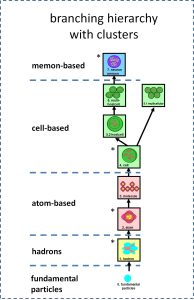
The Third Law of Evolution and the Future of Life. A Systems Approach to Natural Philosophy
Jagers op Akkerhuis G.A.J.M. (2024) Springer. Fig. 5.2, p.92
6 Terminology of the O-theory
Based on fundamental particles as the ‘base level’, and in line with the above triplet of dimensions for ranking hierarchy in nature, the O-theory distinguishes three basic types of systems:
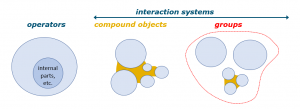
(A) Operator. The dual closure criterion allows one to recognize a group of strictly defined physical countable units called ‘operator’. The operators can be ranked hierarchically according to increasing complexity (upward dimension), where complexity is measured as the number of successive dual closures required to form them.
(B) Interaction system. The O-theory uses the name ‘interaction system’ for any system that consists of interacting operators without itself being classified as an operator. The set of interaction systems can be divided into two major sub-classes: composite objects and groups.
(B1) Composite object. A composite object is a system in which physical interactions between the entities, which are fundamental particles and/or operators and/or composite objects, are stronger than interactions with entities outside the group. The interactions involved typically result from binding forces acting in a space of about the size of the operators involved. Because of such interactions, a compound object is a single countable physical entity. It is possible for a compound object to surround a volume filled with unconnected entities, such as an air bubble in water.
(B2) Group. A group ‘contains’ two or more entities that are either operators or composite objects. Examples of a group are a pile of stones, a herd of cows, molecules in an air bubble in water. In many cases it is the observer who assigns the entities to a group. In some cases, behavioral interactions of organisms can be causal to an active grouping process, e.g. bees in a hive, or people in a company. A group is not a physical thing. It is a theoretical entity, just like a ‘set’.
7 Higher order structure
There is strong evidence to suggest that the operator hierarchy is not just a linear ranking of operators of different types, but that it has a higher-order structure.
The higher order structure is indicated by the following. For example, the operator hierarchy includes two types of operators based on atoms: atoms and molecules. By analogy, four types of operators, bacteria, multicellular bacteria (the blue-green algae), protozoa and plants, are all based on cells. These examples show that the number of possibilities seems to increase between these two groups. These observations suggest a higher order structure of operator theory, which leads to the following hypothesis.
The basic idea is that each dual closure introduces a new property that can be seen to recur at higher levels in the hierarchy. For example, when quarks condensed into larger particles, the hadrons (e.g. protons and neutrons), these were made up of multiple quarks. This was the first appearance of what was called ‘multi-particle’ structure. At higher levels, this property can be seen to recur in molecules (which are multi-atoms), in multicellular bacteria (the blue-green algae) and in eukaryotic multicellular organisms (such as plants). The repeated appearance of the multi-particle configuration along the hierarchy can be compared to black pearls on a necklace. After some white pearls, there is a black pearl. Such recurrence of the multi-particle configuration at increasing distances is one of the properties that suggest that the operator hierarchy has a secondary structure.
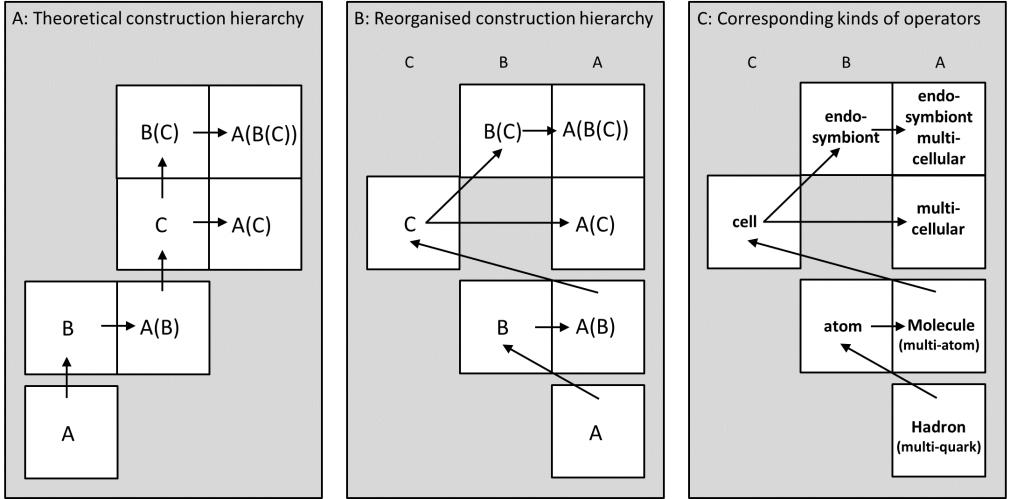
The theoretical arrangement that can be deduced from the above analysis is shown in the following figure. Here the symbols A, B and C denote successively more complex dual closures. Part (a) shows how, in theory, the type of closure from a low-level operator recurs in a more complex form in a higher-level operator. Part (b) shows how the logic of part (a) can be rearranged so that similar types of closure are arranged vertically. Part (c) shows how the principles of parts (a) and (b) work for real examples.
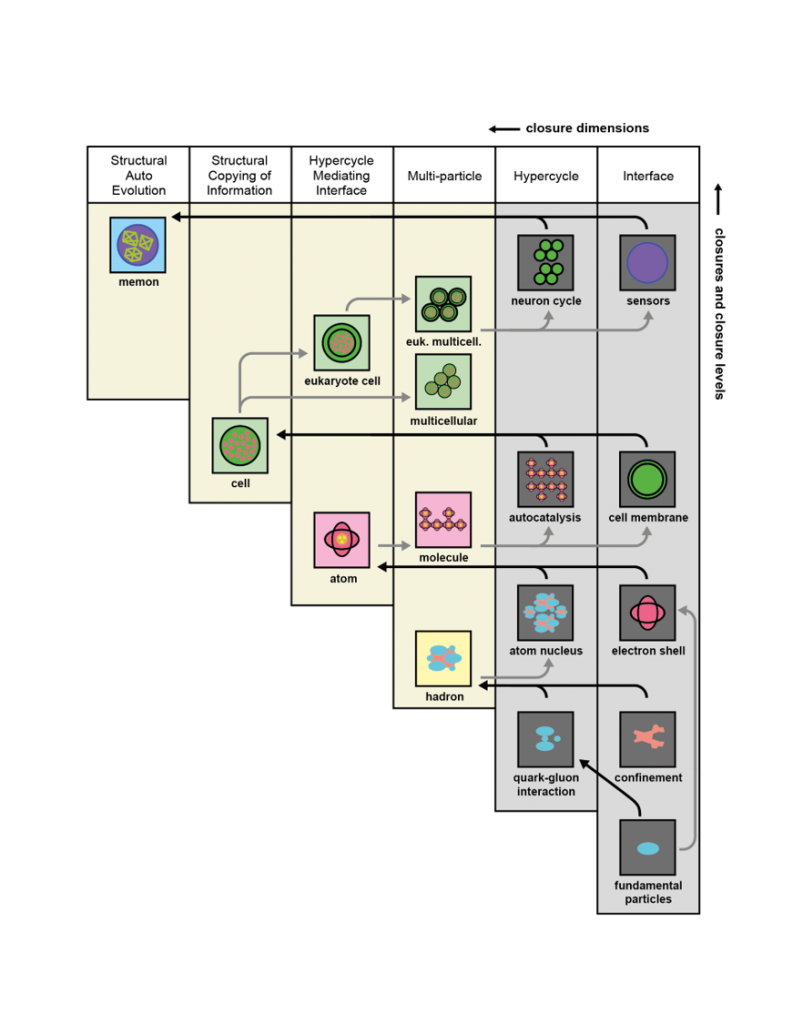
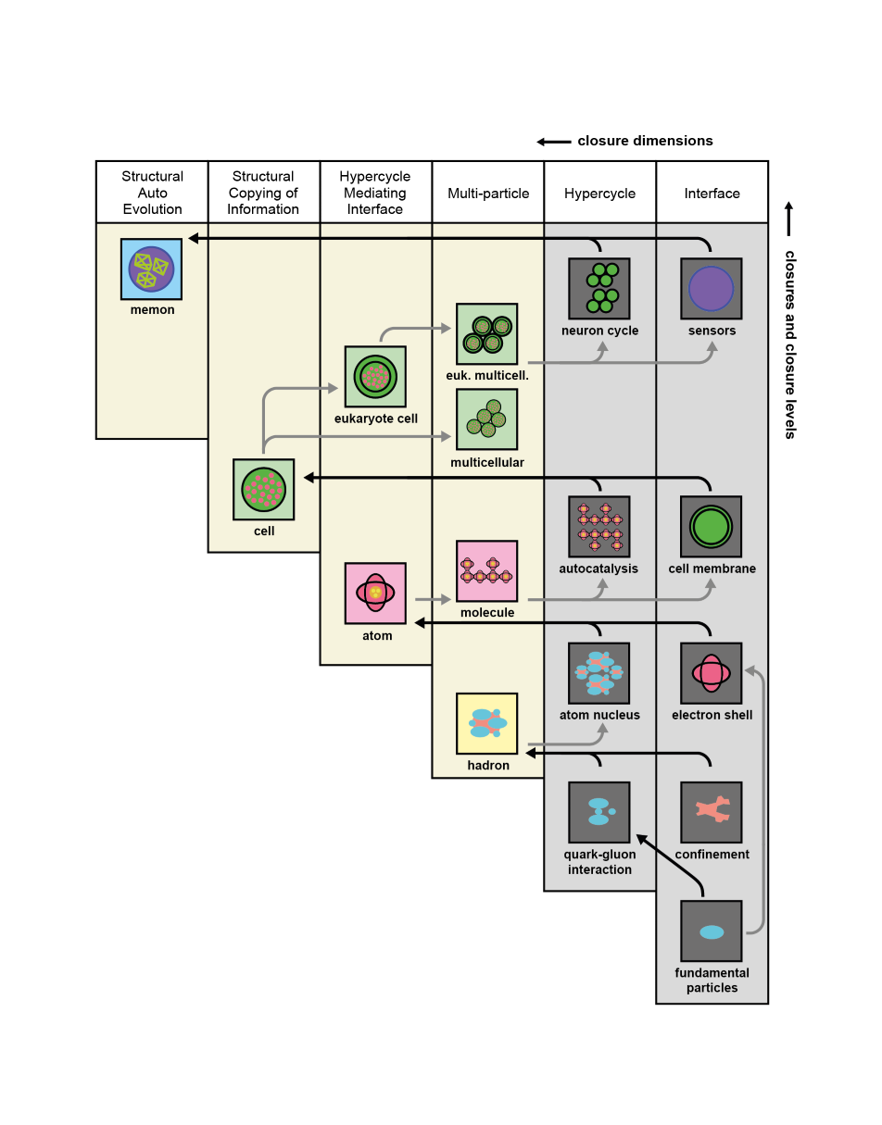
8 The operator hierarchy
The most detailed representation of the operator hierarchy is not limited to operators that all have dual closure, but also includes a number of primitive configurations that have only single closure.
The reason for adding these systems is that some systems at the lower end of the operator hierarchy have only a single closure. For example, hadrons are made up of several quarks, but there is no evidence – as yet – that quarks, or any of the other ‘fundamental particles’ of the ‘Standard Model’, are made up of smaller physical parts. They can be thought of as existing on the basis of a single closure that acts as their interface. When quarks interact, it is on the basis of gluons. Quark gluon interactions can be thought of as a single closure that produces a hypercyclic pattern of interactions. The interface closure and the hypercycle closure together give rise to the operators with the multiparticle property. It would go too far to explain the dimensions of the operator hierarchy in detail (see Chapter 2 of ‘Evolution and transitions in complexity’ (Springer 2016)). Here, I limit the explanation to providing a figure of the entire operator hierarchy, showing its full hypothetical structure.
9 A meta-periodic table
The operator hierarchy can be seen as a periodic table for periodic tables; a meta-periodic table. In fact, the periodicity of the operator hierarchy is not determined by numerical analysis, as is the case with the number of protons and neutrons in an atomic nucleus. Instead, each step in the operator hierarchy also provides a causal path for the formation of operators possessing any next type of dual closure. In this sense, the structure of the operator hierarchy is more than ‘just’ a periodic table.
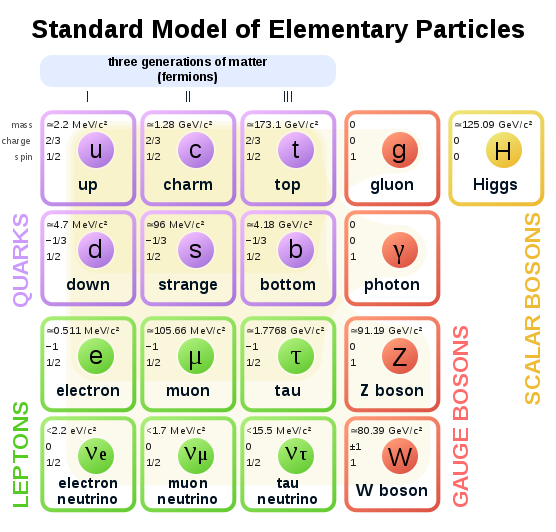
9.1 A periodic table of the fundamental particles: The standard model
Perhaps the most fundamental periodic table is the ‘Standard Model’ of particle physics. It categorises the main classes of fundamental particles as either force-carrying particles (bosons) or matter particles (fermions). Fermions are further divided into leptons and quarks, which are further divided into three groups of increasing mass.
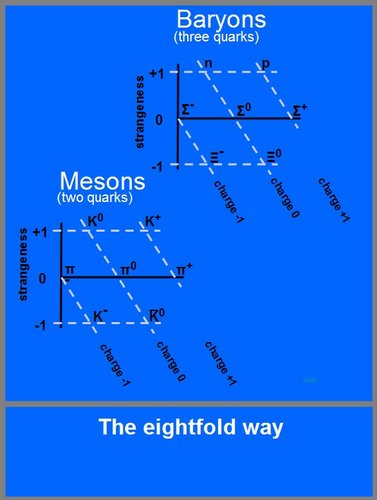
9.2 A periodic table for the hadrons.
Another fundamental periodic table used in particle physics is the ‘eightfold way’. This table is used to organise the many ways in which quarks can combine to form hadrons. Hadrons made up of two quarks are called mesons, while those made up of three quarks are called baryons (‘baryos’ means ‘heavy’), and there is a separate table for each type. The eightfold way was developed by Gell-Mann and Nishijima and received important contributions from Ne’eman and Zweig (Gell-Man and Neeman 1964).
9.3 The periodic table of the elements (Mendeleev 1869)
The best known periodic table is the periodic table of the elements. Of the various proposals, the table proposed by Mendeleev in 1869 has become the most famous. It organised the reactivity of atoms and identified a number of missing elements. The periodic table of the elements is still used as a basic tool in chemistry. Two other tables are directly related to Mendeleev’s periodic table: the ‘nucleotide chart’ and the charts showing which sets of electron shells can be expected in relation to a given number of protons.
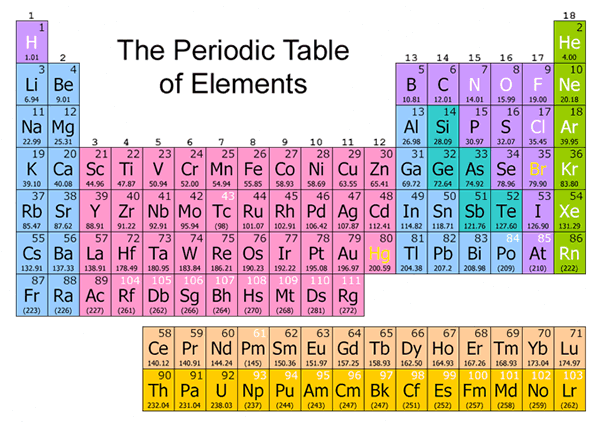
9.4 A periodic table for all molecules
In fact, overviews of many types of molecules exist. However, the number of possible configurations exceeds any attempt to organise them in a limited table.
9.5 A periodic table for the descend of organisms: The tree of life
Finally, although it may be a little unusual to consider this arrangement as a periodic table, there are good reasons to include the ‘tree of life’ in this overview of tabular representations. The only difference with the other tables is that the Tree of Life includes descent, a feature that has no significance in the other periodic tables discussed so far. In all other respects, the Tree of Life provides a unique and meaningful overview of the many different forms of organisms that enter the scheme as species.
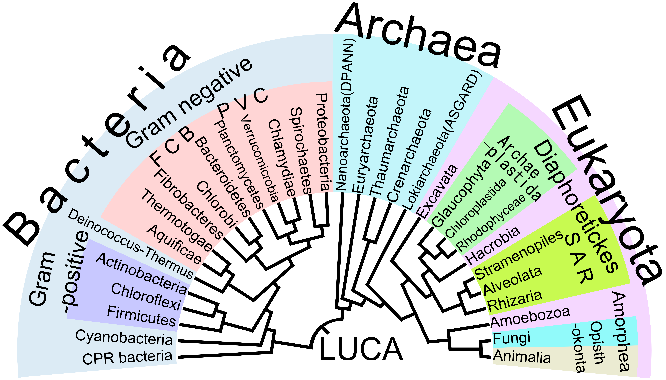
9.6 The OT as a meta-periodic table
The operator hierarchy can be thought of as a periodic table that incorporates a wide range of other periodic tables. In this sense, it is a meta-periodic table.
–
in
